Background Adaptive Work-related Personality Inventory (AWPI) and Adaptive Career Values Inventory (ACI)
Adaptive personality testing: how does it work?
Understanding adaptive testing of cognitive capacities is somewhat more intuitive than adaptive personality testing. In case of adaptive intelligence tests, the following applies: the candidate first responds to a question and is then asked an easier question if the response was wrong, or a more difficult question if the response was right.
The basic concept is the same for personality tests. The characteristics of the question determine whether it is the right question to ask a certain candidate in order to measure someone’s characteristics as quickly and accurately as possible. By only asking those questions that are most relevant to the candidate, the test duration can be significantly reduced.
You can imagine that, in case of personality tests, some questions differentiate more than others, when it comes to higher scores for a certain characteristic, for example.
A good example is wanting to measure the severity of someone’s depression. If you ask the question “I sometimes feel sad” to someone who is severely depressed, this will yield little information; after all, they will certainly agree. In order to make a good diagnosis, it would be better to ask if someone occasionally does not leave bed for an entire day.
Item Response Theory (IRT)
The principles described above originate from the Item Response Theory (IRT, see, for example, Hambleton, Swaminathan, & Rogers, 1991, and Embretson & Reise, 2000). The objective of IRT is to measure the latent (unobserved) score, θ or ‘theta’, of a person on a certain construct (such as intelligence or a personality trait). It is important to mention that IRT models revolve around probability. Given certain characteristics of items (such as the ‘difficulty’ and the degree of discrimination of the item), what is the probability of someone giving a certain reply? The big advantage of IRT is that the characteristics of persons and items can be displayed on the same scale, which allows us to draw conclusions on these probabilities.
The Graded Response Model and category response functions
Most personality inventories (including our WPV and AWPI) use a 5-point Likert scale ranging from Strongly disagree to Strongly agree. Multiple IRT models have been developed for data gained through IRT models. In the AWPI, the Graded Response Model (GRM; Samejima, 1969) is used, which is one of the most frequently used models for responses gained through Likert scales. The basic formula of the GRM is as follows:
/Formule-GRM.png?width=149&height=65&name=Formule-GRM.png)
In the GRM, each item has a parameter (discrimination) and multiple location parameters (d). The number of location parameters equals the number of response categories minus one (so, in case of a 5-point scale, there are four location parameters). But you can forget this formula.
It is more important to remember that the values of a and d are always known in practice: these item characteristics are estimated (“calibrated” in IRT terms) on the basis of research, which is also the case for the AWPI. Since the a and d are known, we can determine the probability of each response for various values of θ. If we enter the various values for θ, we can plot the category response function for each item (see Figure 1 for the category response functions of two Competition items), in which the probability of a certain response is compared to theta.
Figure 1. Category response functions of two items of the Competition scale.
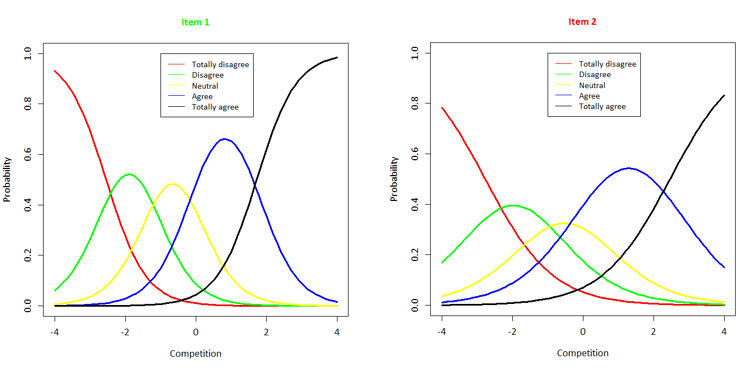 In Figure 1, we see the category response functions of two items of the Competition scale. If we look at Item 1, we can see that, for very low scores (such as -3) the probability of the response ‘Strongly disagree’ is logically the highest. However, as the degree of competitiveness increases, the probability of the ‘Strongly disagree’ response decreases, while the probability of the other responses increases. In case of a below-average degree of Competition (-1), we see that the probability of the ‘Neutral’ response is the highest. If we compare Item 1 and Item 2 to each other, we can also see differences: in case of an above-average degree of competitiveness (2), the probability of ‘Strongly agree’ is the highest for Item 1, while the probability of ‘Agree’ is the highest for Item 2. The items differ in characteristics, which means sometimes one item is better for a certain person, and sometimes another.
In Figure 1, we see the category response functions of two items of the Competition scale. If we look at Item 1, we can see that, for very low scores (such as -3) the probability of the response ‘Strongly disagree’ is logically the highest. However, as the degree of competitiveness increases, the probability of the ‘Strongly disagree’ response decreases, while the probability of the other responses increases. In case of a below-average degree of Competition (-1), we see that the probability of the ‘Neutral’ response is the highest. If we compare Item 1 and Item 2 to each other, we can also see differences: in case of an above-average degree of competitiveness (2), the probability of ‘Strongly agree’ is the highest for Item 1, while the probability of ‘Agree’ is the highest for Item 2. The items differ in characteristics, which means sometimes one item is better for a certain person, and sometimes another.
Item information functions
Whether an item is ‘better’ is determined in terms of IRT by the amount of information an item yields, given a person’s score for a latent trait (such as Competition). The item characteristics of an item determine how much information each item yields for each value of theta. Figure 2 more clearly shows the way this works.
Figure 2. Item information function of two items of the Competition scale.
/Info-voor-in-blog-EN.png?width=500&height=500&name=Info-voor-in-blog-EN.png)
In Figure 2, the information functions are displayed for the same two items of the Competition scales from Figure 1. Two things stand out:
- Usually, Item 1 yields more information than Item 2. In general, this means Item 1 is a ‘better’ item than Item 2.
- Although Item 1 yields more information than Item 2 for most of the values of Competition, this is not always the case. In case of very high Competition values, (approximately > 3) we can see that the line of Item 2 is above that of Item 1: in these situations, Item 2 yields more information than Item 1. In other words, and this complements the example about measuring depression from the introduction, it is better to question someone with a high degree of competitiveness on Item 2 than on Item 1.
This basic principle, showing the item that yields the most information for the given theta, forms the basis of the item selection for the AWPI.
Estimating the latent trait in IRT
Based on the responses a person provided, the latent trait can be estimated. Multiple methods have been developed in the IRT to estimate a person’s latent trait, theta. All methods are, however, based on the probability (or rather the likelihood) of a given response pattern; we find theta where the likelihood of the given response pattern of the person is highest (which is why this estimation method is called ‘maximum likelihood’). However, many adaptive inventories and tests use Bayesian methods to estimate theta; in these methods, the assumption is made that a person (theta) was drawn from a population (in case of one-dimensional IRT, this is the population with a standard normal distribution with an average of 0 and a standard deviation of 1). This standard normal distribution is called the prior, and it is used to measure the likelihood of a certain response pattern. Explaining here how this works in detail goes too far, but in the end the maximum of the new measured likelihood function (the posterior distribution) is the estimated theta (which is why this method is called maximum a posteriori (MAP)). The standard deviation of this posterior distribution indicates the distribution that can be expected around the estimated θ: the smaller this distribution, the more accurate the measurement. This value is called the standard error of measurement (SEM) or standard error. This SEM value is important for adaptive tests and inventories, since this SEM is used as the stop criterium of the test (which also applies to our Adaptive Work-related Personality Inventory (AWPI) and ACT General Intelligence).
Multidimensional IRT (MIRT): the model behind the Adaptive Work-related Personality Inventory
Before, we limited ourselves to one-dimensional IRT, in which only one latent trait was estimated. For the AWPI, we use multidimensional IRT (MIRT), where the objective is to estimate not one, but multiple latent traits at the same time.
There is a large selection of IRT models suitable for multidimensional adaptive testing. The first choice that has to be made is whether between-item multidimensionality or within-item dimensionality is used (Figure 3).
Figure 3. Schematic representation of within-item and between-item dimensionality.
/Figure-between-vs-within.png?width=500&height=331&name=Figure-between-vs-within.png)
In case of between-item multidimensional models, it is assumed that each item is an indicator of only one latent trait (meaning that it is only involved with one trait); multidimensionality is modelled by the correlations between the latent traits (the double-sided arrows on the left side of the figure). It is important to remember that, in case of between-item multidimensionality, the response to a question only depends on one latent trait.
In case of within-item multidimensionality, an item can measure one latent trait or multiple latent traits: above in Figure 3, we can see that item 6 is an indicator of Facet 2 and Facet 3, for example. Within the intelligence domain, this could be an item that measures both reading skills and numeracy. Neither model is necessarily better than the other; it depends on the theoretical model that is applied.
For the AWPI, we have chosen for between-item multidimensionality. This was a pragmatic and practical choice in part: a between-item multidimensional model is straightforward, intuitive, and fits the tradition of factor analysis to use simple structures where an item is only one indicator of a single trait as much as possible. Moreover, a between-item model is consistent with the purpose for which the items were originally developed, namely to measure a single latent trait as optimally as possible. The between-item model is also easier to explain to the end user than a within-item model.
The way MIRT works exactly is complex; whole books have been written on this topic. The most important thing to remember at this moment is that, with multidimensional IRT, estimations can be made more quickly and more accurately than with one-dimensional IRT, because the relationships between the traits that are measured are taken into account. The two most important reasons for this are:
- For one-dimensional IRT, we indicated that, in case of methods like MAP, it is assumed that a person (so theta) is drawn from a population with a normal distribution, with an average of 0 and a standard deviation of 1. In case of the MAP method for MIRT, we assume that a person (multiple thetas at the same time in this case) was drawn from a multivariate distribution with averages equal to µ, and (co)variance matrix Φ. In practice, this prior, meaning the averages µ and (co)variance matrix Φ is estimated based on a very large sample in the calibration phase of the test development. A clear difference between estimating theta(s) in IRT and MIRT is the prior used, which adds information to the likelihood of a response pattern. In case of MIRT, the prior information is much more informative than in IRT.
- This prior is also used during item selection; the prior information is added to the information yielded by each item (see Figure 2). This way, the item is selected which is most relevant for multiple latent traits at the same time at that moment.
Another important difference is that, in case of IRT, only one likelihood function is involved, while in case of MIRT, there are as many functions as thetas to be estimated (in case of the AWPI, this number is 25). The estimation of the thetas using the MAP methods does work the same way for MIRT and IRT: based on a given response pattern, thetas are searched for where the various likelihood functions, measured with the prior, are all simultaneously at a maximum.
In this background article, we have tried to explain the basic principles of adaptive testing, IRT and MIRT for the interested reader. Would you like to know more? Read the technical manuals of the Adaptive Work-related Personality Inventory and the ACT General Intelligence.
Adaptive Work-related Personality Inventory (AWPI)
Based on the basic concepts described above, the AWPI was developed. This adaptive version is based on our Work-related Personality Inventory (WPI), which received a positive assessment from COTAN. This inventory reports on 25 scales and 5 factors; the theoretical basis is the Big Five model. The inventory also reports on 29 competencies.
What is unique about the AWPI is the fact that the inventory is based on the multidimensional model described above. In summary, we can state that, in this model, the relationships between the scales (the prior) are taken into account. We expect that someone who has a high score for Need for Contact will, for example, also have a somewhat higher score on the Socially at Ease scale. The algorithm takes this into account, so estimations can be made more quickly and more accurately. After each answered item, 25 scales are estimated simultaneously. The algorithm looks for the item that provides the most information across the 25 scales.
Figure 4 shows how this works in practice for a candidate.
Figure 4. Example of Adaptive Work-related Personality Inventory in practice.
/Voorbeeldcat-SEM-1-en-2-voor-blog-EN.png?width=750&height=375&name=Voorbeeldcat-SEM-1-en-2-voor-blog-EN.png)
We have only displayed 3 of the 25 scales here, to prevent the figure from becoming too cluttered. In the diagram on the left, we can see the course of the inventory on the X-axis, and the estimations of the scales for Competition, Attentiveness and Self-disclosure on the Y-axis. In the diagram on the right, we can see the progress of the inventory again on the X-axis, and the SEM values, which give an indication of the reliability of the estimated scores, on the Y-axis; the lower the SEM, the more reliable the estimated score. The diagram on the right also shows the end criterium we use in the AWPI, namely the moment the SEM < 0.44 for all scales.
The inventory starts on the basis that all scores are average (which means score 0, the Z scores are of interest here). The inventory starts with a question from the Competition scale. This person responded, ‘Strongly disagree’. You can see the Competition estimation goes down significantly after the first response. Around question 25, the candidate is presented with a Self-disclosure item, to which they respond ‘Strongly disagree’; you can see the Self-disclosure estimation goes down significantly, and the Attentiveness estimation (a scale which corresponds with Self-disclosure) does too, though to a lesser degree. Finally, this person ends with a high score for both Attentiveness and Self-disclosure, scales that, as mentioned before, generally correspond, which is exactly what you see here.
When we view the right diagram, we can see a similar image; the SEM of the scale primarily goes down (or the reliability goes up) when an item of the corresponding scale is questioned. Because of the multidimensional character of the inventory, questions from other scales also yield useful information, which means we find out more about these scales (which, in turn, means the reliability of these scales goes up). Even if no Competition item is asked (such as between item 2 and item 60), the SEM of the Competition scale will slowly go down, because if items from the other scales appear in the questions, we know a little more about how well someone will score on Competition.
All these characteristics of the AWPI allow us to make estimations more quickly and more accurately. Our original full version of the WPV has 276 items, while the adaptive version needs only 90 items on average for equally reliable estimations. This results in a ⅔ reduction of test duration: from 30-40 minutes to about 10-15 minutes. Despite the reduction in test duration, the quality is not affected: research has shown that the AWPI and the WPV are each other’s equivalent.
Adaptive Career Values Inventory (ACI)
Apart from an adaptive inventory for personality, we have also developed an adaptive version of our Career Values Inventory (https://www.ixly.nl/testen/carrierewaarden/). This inventory maps out the motivations of a person, meaning which aspects of a job this person considers motivating. The Career Values Inventory has also received a positive assessment from COTAN.
The basic principles of the ACI are the same as those of the AWPI. We have seen that the adaptive character of the ACI also results in about a ⅔ reduction of the test duration. Research shows that this reduction in test duration does not negatively affect the validity and reliability of the Inventory.
View the Career Values Inventory page.
New adaptive tests in development
In the very short term, the Interest Questionnaire for Tasks and Sectors (ITS) will also receive an adaptive version. The test programmes we have at our disposal (such as the Career Scan) will soon be ready to be applied adaptively. This means that it will be possible to get a broad image of the personality, motivations and interests of a person in about 30 minutes.
